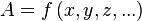Objetivo General:
El estudiante adquirirá destreza en el manejo de técnicas y procedimientos para la solución de problemas. Hará uso de lenguaje matemático de la sistematización de información y de las formas de representación gráfica y analítica. Manejará los conocimientos, métodos y algoritmos matemáticos establecidos en los programas, tanto básicos como auxiliares para abordar los contenidos de otras materias. Elaborará y usará modelos matemáticos en la resolución de problemas de optimización de recursos y en el análisis económico de problemas en el ámbito de las empresas.
MODULO 1
INTRODUCCIÓN AL CÁLCULO EN DOS VARIABLES
Objetivo Particular del Periodo:
El alumno
comprenderá los conceptos básicos del cálculo diferencial en varias variables,
así como la resolución de problemas en el entorno económico-administrativo,
enfatizando aquellos del área de optimización de recursos.
Subtemas:
1.1 Funciones en dos variables.
1.2 Derivadas parciales.
1.3 Máximos y mínimos de funciones de dos variables.
1.4
Aplicaciones: Optimización de funciones de dos variables que representen gastos, ingresos o utilidad. 1.1 Funciones en dos variables.
Definición:
Función de dos variables
Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.
El conjunto de parejas ordenadas para las cuales la regla de correspondencia da un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contra dominio.
Este conjunto de puntos forma una superficie en el espacio tridimensional.
Una función de dos variables se denota usualmente con la notación
z = f (x, y)
Las variables x, y se llaman variables independientes, y z se llama variable dependiente.
La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y,z) en donde (x, y) está en el dominio de f y z = f (x, y).
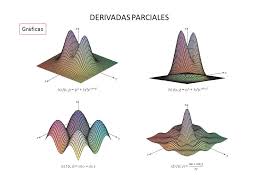
1.2 Derivadas parciales.
En matemática, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud  es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,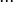 ), es decir:
), es decir:
 es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,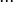 ), es decir:
), es decir:
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función  en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
 en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
EJEMPLO:
Se llama derivada parcial de una función  con respecto a la variable independiente
con respecto a la variable independiente al siguiente límite, si existe y es finito:
al siguiente límite, si existe y es finito:
 con respecto a la variable independiente
con respecto a la variable independiente al siguiente límite, si existe y es finito:
al siguiente límite, si existe y es finito:
calculado suponiendo constante.
constante.
 constante.
constante.
1.3 Máximos y mínimos de funciones de dos variables.
Cálculo de los Máximos y Mínimos de una Función de dos Variables
Valor Máximo Relativo
Es el punto en que la derivada de una función se anula y cambia su valor de positivo a negativo. Es decir la función pasa de creciente a decreciente.
Valor Mínimo Relativo
Es el punto en que la derivada de una función se anula y cambia su valor de negativo a positivo. Es decir la función pasa de decreciente a creciente.
Ejemplos

| 1. | f(x, y) = x - y | Función de dos variables |
| f(1, 2) = 1 - 2 = -1 | Sustituya x por 1 y y por 2 | |
| f(2, -1) = 2 - (-1) = 3 | Sustituya x por 2 y y por -1 | |
| f(y, x) = y - x | Sustituya x por y y y por x |
2. Estudios realizados por una asociación de consumidores en Roma han permitido conformar una función de utilidad con respecto al consumo de servicios de restaurante, influida por las siguientes variables:
x- valoración sobre restaurantes de comida italiana
y- valoración sobre restaurantes de comida internacional
U(x,y) = x³y4- 2x²y³
a-) Calcular las utilidades marginales respecto a cada uno de los dos bienes para
(X0,Y0) = (2,1).
b-) Interprete los resultados.
Solución
a-) U(x,y) = x³y4- 2x²y³

CONCLUSIÓN:
Para concluir este modulo haré una breve explicación de todos los contenidos y el objetivo de la redacción acabada de visualizar, que es utilizar el concepto ya estudiado de funciones de variables como apoyo destacando las diferencias y concordancias.
La derivada de una función de una variable mide la rapidez de cambio de la variable dependiente respecto a la variable independiente.
La optimización de funciones así como su uso en la vida diaria y su aplicación en cada uno de sus elementos como gastos, ingresos y utilidad.
DERECHOS DE AUTOR Y CITAS BIBLIOGRÁFICAS DE UNIDAD lV
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,
DERECHOS DE AUTOR :
Marianela Pastuizaca. (26-MAYO-2011). Cálculo Diferencial - Introducción a funciones de variable real - Sesión 2 1/3. 18-NOV-2015, de YOUTUBE Sitio web: https://www.youtube.com/watch?feature=player_detailpage&v=39CezivMpso.
DERECHOS DE AUTOR:
° Marlon Fajardo Molinares 2009
°McCullans. (1992). Calculo de varias variables. 18-NOV-15, de Editorial Mc Graw Hill Sitio web: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel2.shtml#bibliograa.
DERECHOS DE AUTOR:
Salvador Vera. (2000). Cálculo para la Ingeniería. 18-NOV-15, de GOOGLE Sitio web: http://www.satd.uma.es/matap/svera.
DERECHOS DE AUTOR:
Academatica. (8-08-2013). Máximos y mínimos funciones de dos variables HD. 21-11-2015, de youtube Sitio web: https://www.youtube.com/watch?v=dhhmhSAOEug.
Academatica. (8-08-2013). Máximos y mínimos funciones de dos variables HD. 21-11-2015, de youtube Sitio web: https://www.youtube.com/watch?v=dhhmhSAOEug.