sábado, 21 de noviembre de 2015

MODULO 2 INTEGRACIÓN

MODULO 2

 Integración



DERECHOS DE AUTOR:
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,


Objetivo Particular del Periodo:

El alumno entenderá el concepto de integral y su relación con la derivada. Resolverá problemas de aplicación dando énfasis a aquellos relacionados con las áreas económico-administrativas tales como: Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.

Libro recomendado:

Cálculo integral

Portada


https://books.google.com.mx/books?isbn=8473563166
José Manuel Casteleiro, ‎Rafael Paniagua Gómez-Álvarez - 2002 - ‎





Subtemas:


2.1 Anti derivada.
2.2 Integral indefinida.
2.2.1 Integración con condiciones iniciales.
2.3 Fórmulas básicas de integración.
2.3.1 Integral indefinida de una constante.
2.3.2 Integral de una constante por una variable.
2.3.3 Integral de x  n
2.3.4 Integral de en
2.3.5 Integral de una constante por una función de x.
2.3.6 Integral de una suma (diferencia) de funciones.
2.3.7 Regla de la potencia.
2.3.7.2 Integrales que incluyen funciones exponenciales.
2.3.8 Integrales que incluyen funciones logarítmicas.
2.3.9 Integrales que incluyen (1/u)du
2.3.10 Integrales incluyen au
2.3.11 Integral por partes.
2.4 Aplicaciones: Determinación de funciones de costo, utilidades, consumo, y ahorro a partir de sus marginales. 
  

https://www.youtube.com/watch?v=H3G08Aj0sLE




2.1 Anti derivada

La anti derivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una anti derivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra anti derivada de f(x).
La anti derivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.

Notación
La notación que emplearemos para referirnos a una anti derivada es la siguiente:
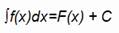
Monografias.com

Ejemplos de anti derivadas

1.
Se toma el exponente y se le suma uno y eso se divide entre el exponente mas uno
despues de hacer las sumas se le suma la constante


2.
Se le agrega la x y la constante

2.2 Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee como "la integral indefinida de f(x) respecto a x" Por lo tanto, f(x) dx es una conjunto de funciones; no es una función sola, ni un número.
La función f que se está integrando se llama el integrando, y la variable x se llama la variable de integración.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.

Propiedades de la integral indefinida

1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx




2.2.1 Integración con condiciones 
iniciales.

Este método es cuando al empezar se le da una condición.
Por ejemplo:

y =2x     para Y= 4x            x=1

                                       2
la integral de 2xdx = 2x     + C
                                     2
               2
F(X) = X    + C
       
        2
4 = 1  + C                4 = 1 + C      4-1 = C              
                                          2
3 = C  entonces  F (X) = x  +3


2.3 Fórmulas básicas de integración.




2.3.1 Integral indefinida de una constante


En cálculo, la integral indefinida de una función dada (es decir, el conjunto de todas las primitivas de la función) se escribe siempre con una constante, la constante de integración.
 Esta constante expresa una ambigüedad inherente a la construcción de primitivas. Si una función f está definida en un intervalo y F es una primitiva de f, entonces el conjunto de todas las primitivas de f viene dado por las funciones F (x) + C, siendo C, una constante arbitraria.
La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque (F + C) ‘ = F ‘ + C ‘ = F ‘ + 0 = F ‘. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.
Para interpretar el significado de la constante de integración se puede observar el hecho de que la función f (x) es la derivada de otra función F (x), es decir, que para cada valor de x, f(x) le asigna la pendiente de F (x). Si se dibuja en cada punto (x, y) del plano cartesiano un pequeño segmento con pendiente f (x), se obtiene un campo vectorial como el que se representa en la figura de la derecha. Entonces el problema de encontrar una función F (x) tal que su derivada sea la función f (x) se convierte en el problema de encontrar una función de la gráfica de la cual, en todos los puntos sea tangente a los vectores del campo. En la figura de la derecha se observa como al variar la constante de integración se obtienen diversas funciones que cumplen esta condición y son traslaciones verticales unas de otras.



2.3.2 Integral de una constante por una variable.

La integral de una constante es igual a la constante por x.

integral de una constante

Ejemplo

integral de una constante

Integral de cero

integral de cero

Para integrar Una constante J que multiplica a dx se recomienda primero sacar el factor J y multiplicarlo por lo que quedó de la integral, en este caso dx.
∫Jdx
La integral dx podemos entender que es la integral de uno ya que siempre se puede integrar uno y no afecta el valor de la integral
∫Jdx=Jdx
 ∫Jdx=J1*dx
 El resultado va a ser dejar la constante y multiplicarka por el resultado de esta integral que en este caso es x
 ∫Jdx=J1*dx=J[x]
 Para finalizar al resultado se le debe aregar un constante aleatoria
 ∫Jdx=J1*dx=J[x]+c
Esto sería la regla de integración de una itegral J que multiplica a dx.
De manera general utilizando la misma idea, la integral de cualquier constante, pero ahora multiplicada por el diferencial de una función u: 
∫Jdu
No necesariamente debe ser x el resultado puede ser también sacar la constante y multiplicarla por el diferencial de u 
∫Jdu
∫Jdu=J∫du=J[u]+c
 Ejemplos:
 ∫-12dx=-12∫dx
=-12[x]+c
=-12+c


2.3.3 Integral de x  n



https://www.youtube.com/watch?v=JdsgI7lXoNk




2.3.4 Integral de e n

integral exponencial





2.3.5 Integral de una constante por una función de x

La derivada de cualquier función constante es cero. Una vez se ha encontrado una primitiva F, sumándole o restándose una constante C se obtiene otra primitiva, porque (F + C) ' = F ' + C ' = F'. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.
Por ejemplo, su póngase que se quiere encontrar las primitivas de cos(x). Una de estas primitivas es sin(x). Otra es sin(x)+1. Una tercera es sin(x)-π. Cada una de estas funciones tiene por derivada cos(x), por lo tanto todas son primitivas de cos(x). Resulta que añadir y restar constantes es el único grado de libertad que hay al encontrar primitivas diferentes de la misma función. Es decir, todas las primitivas son las mismas con la diferencia de una constante. Para expresar este hecho para cos(x), se escribe:
\int \cos(x)\,dx = \sin(x) + C.
Sustituyendo C por un número cualquiera, se obtiene una primitiva. En cambio, escribiendo C en vez de un número se obtiene una descripción compacta de todas las primitivas posibles de cos(x). C se denomina constante de integración. Se puede comprobar fácilmente que todas estas funciones son, en efecto, primitivas de cos(x): 

{d\over dx}[\sin(x) + C]= {d\over dx}[\sin(x)] + {d\over dx}(C)
= \cos(x) + 0\,
= \cos(x)\,.







2.3.6 Integral de una suma (diferencia) de funciones

La integral de la suma de dos funciones es la suma de las integrales de las funciones individuales, y la integral de la diferencia de dos funciones es la diferencia de las integrales de las funciones individuales. 



2.3.7 Regla de la potencia

Regla de Potencias

La derivada de una potencia o función potencial, es igual al exponente por la base elevada al exponente menos uno y por la derivada de la base.


Te presento 5 ejercicios para tu práctica:
  • f(x) = -2x³
  • f(x) = 12²
  • y = 3x³+2x²+x
  • y = 29x³+2x²-12x
  • y = 45x²
Estos ejercicios te ayudaran a comprender y representar de mejor manera la regla de potencias, efectúelos para encontrar el producto de la misma y asi lograr un buen programa de aprendizaje.



2.3.7.2 Integrales que incluyen funciones exponenciales
La siguiente es una lista de integrales de funciones exponenciales 

\int e^{cx}\;dx = \frac{1}{c} e^{cx}

\int xe^{cx}\; dx = \frac{e^{cx}}{c^2}(cx-1)

\int x^2 e^{cx}\;dx = e^{cx}\left(\frac{x^2}{c}-\frac{2x}{c^2}+\frac{2}{c^3}\right)
\int x^n e^{cx}\; dx = \frac{1}{c} x^n e^{cx} - \frac{n}{c}\int x^{n-1} e^{cx} dx


2.3.8 Integrales que incluyen funciones logarítmicas

Integrales Logarítmicas


integral


integral exponencial




2.3.9 Integrales que incluyen (1/u)du



2.3.11 Integral por partes


INTEGRACIÓN POR PARTES




El método de integración por partes está basado en la derivada de un producto  de funciones como se muestra a continuación

d(u.v) = u dv + v du

por eso es que se usa para integrales que contienen dos funciones que se multiplican entre si.


∫d(u.v) = ∫u dv + ∫v du   (se integra en ambos lados de la fórmula)


(u.v) = ∫u dv + ∫v du (resolviendo la integral)

∫u dv = u v - ∫v du (despejando, queda la fórmula de  la integración por partes)

Se llama integración por partes, porque la integral se divide en dos partes una u y otra dv. La integral debe estar completa y sin alterar la operación dentro de ella. Esta selección es lo más importante y se debe realizar de la siguiente manera


1.- En la parte que corresponde a dv debe ser la función más fácil de integrar,
2.- En u deben ir  aquellas funciones que no tienen integral directa (funciones logarítmicas e inversas), luego se pueden considerar las funciones algebraicas puesto que la derivada  es reductiva. Las funciones trigonométricas y exponenciales son más sencillas de trabajar.

Una de las reglas para   saber si  el procedimiento realizado es correcto  la integral resultante debe ser más sencilla que la original o sino de igual dificultad.

CONCLUSIÓN:
Como conclusión se puede definir que la integración es un concepto fundamental de las matemáticas avanzadas, especialmente en los campos del cálculo y del análisis matemático. Básicamente, una integral es una suma de infinitos sumandos, infinitamente pequeños convirtiéndolos en un todo. 
En el campo de la administración equivalentemente hablando la concepción seria la misma agregándole la lógica, la describiría como la sumatoria ú ordenamiento inteligente de todos los parámetros operacionales concatenados eficientemente entre recursos humanos y logísticos con el objetivo de alcanzar un bien en común necesario para mejorar nuestra sociedad.

DERECHOS DE AUTOR:
cetremo14. (8-dic-2011). Cálculo Integral - Tutorial de Integración Básica. 21-11-2015, de www.youtube.com Sitio web: https://youtube/H3G08Aj0sLE.

DERECHOS DE AUTOR:
Camila Silva A.. (julio 2009). ANTIDERIVADAS. 21-11-2015, de monografias.com Sitio web: http://www.monografias.com/trabajos73/antiderivadas/antiderivadas.shtml

DERECHOS DE AUTOR:
vitutor. (2011 agosto, 8). Integral indefinida. 1/11/2015, de Ecured Sitio web: http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html.

DERECHOS DE AUTOR:
Stewart, James . (2008). Constante de integración. 21-11-2015, de Wikipedia,la enciclopedia libre Sitio web: https://es.wikipedia.org/wiki/Constante_de_integraci%C3%B3n.

DERECHOS DE AUTOR:
Bersaín Lejarza Abelleyra. (julio de 2005). INTEGRAL DE UNA CONSTANTE Y DE UNA FUNCIÓN A UNA POTENCIA. 21-11-2015, de WWW.BLOGSPOT.COM Sitio web: libretadesalon.blogspot.com/.../integral-de-una-constante-y-de-una.html.

DERECHOS DE AUTOR:
Tareasplus . (1-11-2011). Integral mediante serie de potencias de e a la x al cuadrado. 21-11-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=PUyQSaV_ex4.

DERECHOS DE AUTOR:
KhanAcademyEspanol. ( 3 abr. 2013). Integral indefinida de x elevada a una potencia. 21-11-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=JdsgI7lXoNk.

DERECHOS DE AUTOR:
math2me. (07-feb-2012). Integral de la suma o resta de funciones - HD. 21-11-2015, de www.youtube.com Sitio web: https://www.youtube.com/watch?v=yn_hFO6W6Jk&feature=youtu.be






Publicado por en

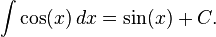
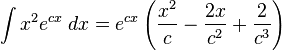
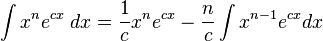
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)