MODULO 3
Integral Definida
DERECHOS DE AUTOR:
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,
Subtemas:
3.1 Área bajo la curva.
3.2 Teorema Fundamental del cálculo.
3.3 Propiedades de la integral definida.
3.4 Área entre una y dos curvas.
3.5 Aplicaciones: Excedente del consumidor y del productor, valor presente y valor futuro.
3.1 Área bajo la curva.
Refiriéndonos a la historia, el cálculo integral se dio a la luz gracias al problema geométrico de hallar áreas de regiones no poligonales, es decir de regiones con aspecto curvo (imagínenselo por ustedes mismos). De hecho, vamos a mostrar, -no como los antiguos griegos-pero de la forma mas moderna, el como podemos hallar áreas haciendo uso de la integral. Comencemos dando una primera definición de la relación que existe entre la integral y el área (bajo curva en primera medida) de una región no poligonal:
ÁREAS BAJO CURVA
Definición: Sí f es continua y no negativa en un intervalo cerrado , el área de la región limitada por la gráfica de f, el eje x y las rectas verticales viene dada por:
ÁREA = ∫ f(x)dx
Observemos la siguiente FIG 1:
En ella se ve que f es una función continua, positiva (por encima del eje x), y la región R está limitada (acotada) por las rectas verticales x=a y x=b. Podemos hallar el área de la región R por medio de una integral definida aplicando la definición anterior.
ÁREAS BAJO CURVA
Definición: Sí f es continua y no negativa en un intervalo cerrado , el área de la región limitada por la gráfica de f, el eje x y las rectas verticales viene dada por:
ÁREA = ∫ f(x)dx
Observemos la siguiente FIG 1:
En ella se ve que f es una función continua, positiva (por encima del eje x), y la región R está limitada (acotada) por las rectas verticales x=a y x=b. Podemos hallar el área de la región R por medio de una integral definida aplicando la definición anterior.
3.2 Teorema Fundamental del cálculo
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
(EL PRIMER TEOREMA FUNDAMENTAL DEL CÁLCULO) Sea f una función integrable en [a,b], y definimos una nueva función F en [a,b] por
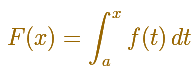
Si c pertecece a [a,b] y f es continua en c, entonces F es diferencial en c, y
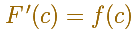
Una demostración visual bien conocida asume que la función f es continua en un entorno del punto (esta es una condición más débil, la hipótesis del teorema es más fuerte. Para una demostración analítica más rigurosa de este teorema hay que leer un buen libro de Cálculo).
Si c es un punto de (a,b), mirando la imagen podemos aceptar que
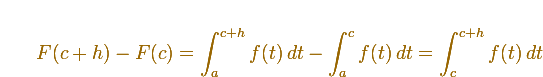
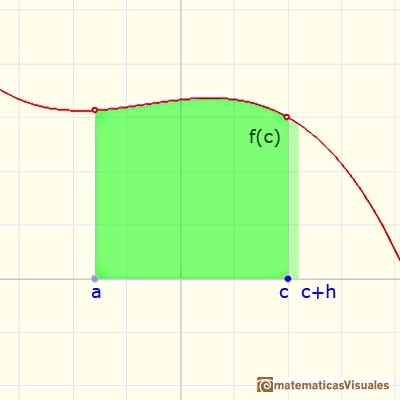
3.3 Propiedades de la integral definida
Se enuncian algunas propiedades y teoremas básicos de las integrales definidas que ayudarán a evaluarlas con más facilidad.
1) 
donde c es una constante.
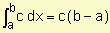donde c es una constante.
2) Si f y g son integrables en [a, b] y c es una constante, entonces las siguientes propiedades son verdaderas:
(se pueden generalizar para más de dos funciones)
3) Si x está definida para x = a entonces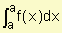 
= 0
= 0
4) Si f es integrable en [a, b] entonces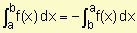 
5) Propiedad de aditividad del intervalo: si f es integrable en los dos intervalos cerrados definidos por a, b y c entonces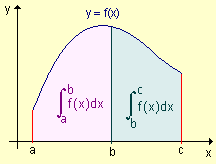  
3.4 Área entre una y dos curvas.
En esta sección estudiaremos como calcular el área entre dos curvas.
El problema es el siguiente: Dadas dos funciones f y g , encontrar el área contenida entre sus gráficas en el intervalo [a,b] .
Para ilustrar el problema y el procedimiento, observa el siguiente ejemplo.
| ||||||
https://youtu.be/ljWj8QgQAa4
CONCLUSIÓN:
CONCLUSIÓN:
De forma resumida cuando estudiamos el problema del área y el problema de la distancia analizamos que tanto el valor
del area debajo de la grafica de una funcion como la distancia recorrida por un objeto se puede calcular
aproximadamente por medio de sumas o bien exactamente como el limite de una suma.
analizamos
DERECHOS DE AUTOR:
julioprofe. (1-MAYO-2009). Área bajo una curva - Ejercicio 1. 21-11-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=V7WnsXYJZaM.
DERECHOS DE AUTOR:
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc. Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc. Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press. (1963). El teorema fundamental del calculo. 21-nov-2015, de Matematicas visuales Sitio web: www.matematicasvisuales.com/html/analisis/ftc/ftc1.html.
DERECHOS DE AUTOR:
Tareasplus. (15-JUNIO-2012). Integral definida y sus propiedades básicas. 21-NOV-2015, de WWW.YOUTUBE.COM Sitio web: https://youtu.be/L4K4JXMXJbI.
No hay comentarios:
Publicar un comentario