


DERECHOS DE AUTOR:
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,
MODULO 4
Jagdish C. Arya Robin W. Lardner Víctor Hugo Ibarra Mercado. ( 1993). MATEMÁTICAS APLICADAS a la administración y a la economía. EN MEXICO,Estado de Mexico: Pearson Education,
MODULO 4
Sistemas de ecuaciones lineales y matrices
Objetivo Particular del Periodo:
El alumno entenderá los conceptos
elementales del álgebra lineal y los aplicará en problemas del ámbito económico
y de gestión de negocios.
Subtemas:
4.1 Sistemas de ecuaciones
lineales.
4.1.1 Definición
4.1.2 Sistemas de ecuaciones
lineales: consistentes, inconsistentes, y su representación para métrica del
conjunto solución.
4.1.3 Métodos para resolución
de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución,
eliminación (sumas y restas).
4.1.4 Sistemas de ecuaciones
equivalentes.
4.1.5 Eliminación de Gauss y
Gauss-Jordan.
4.1.5.1 Definición de matriz.
4.1.5.2 Expresión
matricial de un sistema de ecuaciones lineales.
4.1.5.3 Operaciones elementales sobre
renglones.
4.1.5.4 Reducción de Gauss y
Gauss-Jordan.
4.1.5.5 Sistemas homogéneos.
4.2 Álgebra de
Matrices
4.2.1 Tipos de matrices (cuadrada,
rectangular, triangular, matriz identidad, matriz transpuesta).
4.2.2 Operaciones con matrices (suma,
diferencia, multiplicación por escalar y producto de matrices).
4.2.3 Propiedades de las operaciones con
matrices.
4.2.4 Matriz
inversa.
4.3 Determinantes
4.3.1 Definición de un determinante.
4.3.2 Expansión por cofactores.
4.3.3 Propiedades
de los determinantes.
4.3.4 Regla de Cramer.
4.4
Aplicaciones: Modelo insumo-producto, análisis de ventas y comportamiento del
consumidor.
4.1 Sistemas de ecuaciones lineales.
1. Ecuaciones con dos incógnitas.
En este apartado vamos a tratar con ecuaciones con dos incógnitas. Por ejemplo, 2x - 5y = 7 es una ecuación con dos incógnitas.
El par de valores x = 6, y = 1 es solución de esta ecuación porque 2 · 6 - 5 · 1 = 7.
Definición: Llamamos solución de una ecuación con dos incógnitas a todo par de valores que hacen cierta la igualdad. Cabe destacar que si sólo tenemos una ecuación con dos incógnitas, tendremos infinitas soluciones.
Las ecuaciones lineales se representan mediante rectas.
Para obtener las soluciones de dos incógnitas se despeja una de ellas y se le dan valores a la otra. Si representamos las dos ecuaciones que forman un sistema como dos rectas, se puede observar que el punto donde se cortan dichas rectas (si se cortan) es la solución al sistema.
Ejemplo:

Tabla de la 1ª Ecuación
Tabla de la 2ª Ecuación
Representación gráfica de ambas ecuaciones. Aquí podemos observar cómo la solución del sistema es x=4 e y=1
2. Sistemas de ecuaciones.
Definición: Dos ecuaciones forman un sistema cuando lo que pretendemos de ellas es encontrar su solución común. Cuando dos ecuaciones con dos incógnitas forman un sistema, las ponemos de esta forma:

Se llama solución de un sistema de ecuaciones a la solución común de ambas.
3. Sistemas equivalentes.
Definición: Dos sistemas de ecuaciones se dicen equivalentes cuando tienen la misma solución.
4. Número de soluciones de un sistema lineal.
4.1. Sistemas sin solución.
Hay sistemas cuyas ecuaciones dicen cosas contradictorias. Por ejemplo:

En este caso, nos dice por una parte que 2x+3y=15 y por otra que 2x+3y=9 y eso es absolutamente imposible porque para eso tendrían que adoptar las incógnitas valores distintos en cada ecuación y entonces no sería un sistema de ecuaciones.
Así sacamos la conclusión de que el sistema no tiene soluciones comunes y entonces se dice que el sistema es incompatible.
4.2. Sistemas con infinitas soluciones.
Hay sistemas cuyas ecuaciones dicen lo mismo o que una ecuación es proporcional a la otra, es decir, tenemos dos veces la misma ecuación. Veamos un ejemplo:

(1)

(2)
En el ejemplo (1) tenemos que las dos ecuaciones son idénticas y en el ejemplo (2) tenemos que la segunda ecuación es la misma, pero multiplicada por 2, entonces si dividimos toda la ecuación por 2, obtendremos de nuevo que tenemos dos ecuaciones idénticas.
En este caso el sistema se llamará compatible determinado, porque tiene soluciones, pero éstas son infinitas.
4.1.1 Definición
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo.

4.1.2 Sistemas de ecuaciones lineales: consistentes, inconsistentes, y su representación para métrica del conjunto solución.
Clasificación de los sistemas de ecuaciones lineales y tipos de soluciones
Una ecuación lineal es una ecuación algebraica que contiene variables cuyo máximo grado posible es uno. Tales ecuaciones se utilizan normalmente para definir líneas rectas. Cuando tenemos numerosas ecuaciones lineales, donde sus posibles soluciones nos dan un punto de solución, las llamamos como conjunto, sistema de ecuaciones lineales. Generalmente, un sistema de ecuaciones lineales se convierte en forma de matriz por conveniencia para su solución. Sea un sistema de ecuaciones lineales dado como, x + y – z = 1 3x – 2y + z = 3 4x + y – 2z = 9
A continuación se indica la forma matricial del sistema de la ecuación como,

Existen tres tipos de sistemas de ecuaciones lineales posibles, los cuales dependen del punto de intersección de la ecuación lineal en un determinado sistema de ecuación. Estos son:
1. Inconsistente independiente: Si las ecuaciones del sistema dado vienen a ser las mismas rectas que difieren en su pendiente, entonces tal sistema de ecuaciones lineales es llamado consistente y dependiente. Este sistema de ecuaciones lineales no proporciona una solución dado que todas las rectas son paralelas entre sí y no pueden cumplir con los demás, incluso si se extiende hasta el infinito, por lo que nunca se obtiene un punto de intersección, y por tanto, no puede obtenerse ninguna solución.

2. Consistente dependiente: Si todas las ecuaciones en un sistema de ecuaciones lineales calculan la misma recta en un pedazo de papel milimetrado, de manera que todas las rectas se superpongan unas sobre otras, podemos llamar a tal sistema de ecuaciones como un sistema de ecuaciones lineales inconsistente e independiente. En este caso obtenemos un número infinito de soluciones porque todos los puntos por encima de la recta son puntos de intersección.

3. Consistente independiente: Este es el sistema más general de las ecuaciones lineales, donde tenemos un número de rectas que se interceptan en un solo punto, el cual es la única solución para el sistema de ecuaciones, y denominamos a tal sistema de ecuaciones consistente e independiente.

Además de esto también tenemos tres categorías de posibles soluciones para un determinado sistema de ecuaciones lineales. Estas son:
1. Solución Independiente: La solución independiente es la solución única para un sistema de ecuaciones lineales. Para un sistema de ecuación, si aplicamos una operación de transformación de fila generalmente obtendremos una matriz de identidad. Una característica única de este tipo solución es que se necesita disponer de tantos números de ecuaciones como variables en el sistema dado. Si este requisito no se cumple, no podemos obtener una solución independiente.

Al resolver el sistema de ecuaciones obtenemos una solución única para cada una de las tres variables como x = 3, y = 1 y z = 2
2. Solución Dependiente: La solución dependiente es aquella por medio de la cual se obtienen numerosas soluciones para una sola variable, este es el caso de las soluciones múltiples. Para este sistema de ecuaciones, si aplicamos la operación de transformación de fila generalmente obtendremos pocos términos de cero. Usualmente, es el caso donde el número de variables es mayor que el número de ecuaciones en el sistema. Muchas veces este sistema contiene una fila cero.

La solución del sistema es x = 4 - 3t, y = 3 + 2t, z = t.
3. Solución Inconsistente: La solución es inconsistente, cuando no obtenemos ninguna solución para el sistema de ecuaciones lineales.

No tenemos una solución para el sistema de ecuaciones anterior.
4.1.3 Métodos para resolución de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución, eliminación (sumas y restas).
Para mejor entendimiento de este tema véase la siguiente presentación.
4.1.4 Sistemas de ecuaciones equivalentes.
| CRITERIOS DE EQUIVALENCIA DE SISTEMAS DE ECUACIONES LINEALES. |
Se dice que dos sistemas de ecuaciones lineales son equivalentes cuando tienen las mismas soluciones, es decir, toda solución del primero lo es también del segundo y, recíprocamente, cada solución del segundo es también solución del primero.
Conviene destacar que dos sistemas de ecuaciones equivalentes no tienen que tener el mismo número de ecuaciones, aunque si es necesario que tengan el mismo número de incógnitas.
Criterio 1: Si se multiplican o dividen los dos miembros de una ecuación de un sistema por un número real distinto de cero, se obtiene otro sistema equivalente al inicial.
Ejemplo: Los siguientes sistemas son equivalentes, puesto que para pasar del primero (azul) al segundo (rojo), multiplicamos la primera ecuación por 3, la segunda ecuación por 2 y la tercera por -1.

Criterio 2: Si a una ecuación de un sistema se le suma o resta otra ecuación del mismo, se obtiene otro sistema equivalente al inicial.
Ejemplo: Los siguientes sistemas son equivalentes, puesto que para pasar del primero (azul) al segundo (rojo), a la segunda ecuación le restamos la primera.

Criterio 3 (fusión de los anteriores): Si a una ecuación de un sistema se le suma o resta otra ecuación del mismo, multiplicada por un número real distinto de cero, se obtiene otro sistema equivalente al dado.
Ejemplo: Los siguientes sistemas son equivalentes, puesto que para pasar del primero (azul) al segundo (rojo), a la segunda ecuación le restamos la primera multiplicada por 3 y a la tercera ecuación le restamos la primera multiplicada por 2.

Criterio 4: Si en un sistema de ecuaciones lineales una ecuación es proporcional a otra o es combinación lineal de otras, se puede suprimir y el sistema obtenido es equivalente al inicial.
Por lo tanto, antes de discutir o resolver un sistema de ecuaciones lineales, es conveniente suprimir las ecuaciones superfluas que se puedan identificar fácilmente, como, por ejemplo:
Ejemplo: Los siguientes sistemas son equivalentes pues se suprimió la tercera ecuación, que era proporcional a la primera (la tercera ecuación es igual a la primera ecuación multiplicada por 3).

Ejemplo: Los siguientes sistemas son equivalentes pues se suprimió la segunda ecuación, ya que todos los coeficientes y el término independiente de la misma son nulos.

Ejemplo: Los siguientes sistemas son equivalentes pues se suprimió la cuarta ecuación, que era la suma de las ecuaciones primera y segunda.

Es obvio, además, que si en un sistema de ecuaciones lineales cambiamos el orden de las ecuaciones, el sistema obtenido es igual al anterior. El sistema tampoco cambia si en todas las ecuaciones del mismo, permutamos el orden de las incógnitas.
Ejemplo: Los siguientes sistemas son iguales, pues sólo permutó el orden de la ecuaciones primera y tercera.

Ejemplo: Los siguientes sistemas son iguales, pues sólo permutó, en todas las ecuaciones, el orden de las incógnitas x e y.

La aplicación de estos criterios de equivalencia de sistemas de ecuaciones lineales, facilitará la obtención de otro sistema equivalente al inicial, que sea más sencillo de resolver.
|
4.1.5 Eliminación de Gauss y Gauss-Jordan.
En matemáticas, la eliminación de Gauss-Jordan, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.
EJEMPLO:
Supongamos que es necesario encontrar los números "x", "y", "z", que satisfacen simultáneamente estas ecuaciones:
Esto es llamado un sistema lineal de ecuaciones. El objetivo es reducir el sistema a otro equivalente, que tenga las mismas soluciones. Las operaciones (llamadas elementales) son estas:
- Multiplicar una ecuación por un escalar no nulo.
- Intercambiar de posición dos ecuaciones
- Sumar a una ecuación un múltiplo de otra.
Estas operaciones pueden representarse con matrices elementales que se usan también en otros procedimientos como la factorización LU o la diagonalización por congruencia de una matriz simétrica.
En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:
Ahora eliminamos y de la primera ecuación sumando -2 veces la segunda ecuación a la primera, y sumamos -4 veces la segunda ecuación a la tercera para eliminar y.
Finalmente eliminamos z de la primera ecuación sumando -2 veces la tercera ecuación a la primera, y sumando 1/2 veces la tercera ecuación a la segunda para eliminar z.
Despejando, podemos ver las soluciones:
Para clarificar los pasos, se trabaja con la matriz aumentada. Podemos ver los 3 pasos en su notación matricial:
Primero:
Después,
Por último.
Si el sistema fuera incompatible, entonces nos encontraríamos con una fila como esta:
Que representa la ecuación: 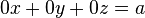 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 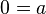 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.
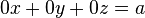 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 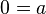 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.
4.2 Álgebra de Matrices
Puede ser una matriz con valores
O también una matriz con índices (Genérica)
Puede ser de otro tamaño e incluso con variables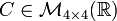
La matriz identidad puede ser de cualquier tamaño, siempre y cuando sea cuadrada.
4.2.2 Operaciones con matrices (suma, diferencia, multiplicación por escalar y producto de matrices).
4.2.3 Propiedades de las operaciones con matrices.
4.2.4 Matriz inversa.






4.3.1 Definición de un determinante

Leer más: http://www.monografias.com/trabajos101/determinates-algebra-lineal/determinates-algebra-lineal.shtml#ixzz3sFEh1nDU
4.3.2 Expansión por cofactores.

 Esto se puede ver de la fórmula de . Empleando la siguiente identidad
Esto se puede ver de la fórmula de . Empleando la siguiente identidad
4.3.4 Regla de Cramer
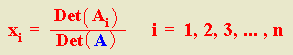

En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. La notación de una matriz  tiene la forma:
tiene la forma:
 tiene la forma:
tiene la forma:
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
4.2.1 Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta).
Matriz cuadrada
Se dice que una matriz A es cuadrada si tiene el mismo número de filas que de columnas. Ejemplos de matriz cuadrada:
Puede ser una matriz con valores

O también una matriz con índices (Genérica)

Puede ser de otro tamaño e incluso con variables
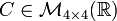
Se llama diagonal principal de una matriz A a la diagonal formada por los elementos 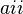 .
.
Se llama diagonal secundaria a la diagonal del cuadrado que no es la principal, tiene por extremos los elementos y
y 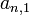 , como características, todos los elementos tienen la particularidad que sus índices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus índices suman (n+1), por ejemplo 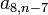 , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.
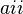 .
.Se llama diagonal secundaria a la diagonal del cuadrado que no es la principal, tiene por extremos los elementos
 y
y 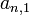 , como características, todos los elementos tienen la particularidad que sus índices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus índices suman (n+1), por ejemplo 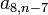 , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.Matriz Rectangular
Es aquella matriz que no es cuadrada, esto es que la cantidad de filas es diferente de la cantidad de columnas.
Puede ser de dos formas; vertical u horizontal.
Puede ser de dos formas; vertical u horizontal.
Matriz Triangular superior
Se dice que una matriz (cuadrada) es triangular superior si todos los elementos que están por debajo de la diagonal principal son nulos.
Matriz Triangular inferior
Se dice que una matriz es triangular inferior si todos los elementos que están por encima de la diagonal principal son ceros.
Matriz Identidad
Se llama matriz identidad de orden n y se nota In a una matriz cuadrada de orden n en la que los elementos de la diagonal principal son 1 y el resto 0.
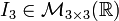
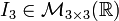
La matriz identidad puede ser de cualquier tamaño, siempre y cuando sea cuadrada.
Matriz Traspuesta
Matriz traspuesta (At). Se llama matriz traspuesta de una matriz A a aquella matriz cuyas filas coinciden con las columnas de A y las columnas coinciden con las filas de A.
- Para una matriz
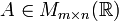 , se define la matriz transpuesta de
, se define la matriz transpuesta de  , denotada por
, denotada por 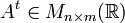 , como
, como 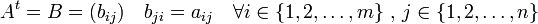 . Es decir, las filas de la matriz
. Es decir, las filas de la matriz  corresponden a las columnas de
corresponden a las columnas de  y viceversa.
y viceversa.
4.2.2 Operaciones con matrices (suma, diferencia, multiplicación por escalar y producto de matrices).
4.2.3 Propiedades de las operaciones con matrices.
Dadas dos matrices A = (aij) y B = (bij) de dimensión m x n, la matriz A + B es otra matriz S = (sij) de la misma dimensión, de modo que cada elemento sij de la matriz S, se obtiene como: sij = aij + bij. Es decir, para que dos matrices A y B se puedan sumar tienen que tener la misma dimensión y, en este caso, se suman los elementos que ocupan la misma posición.
| |
 | |
PROPIEDADES DE LA SUMA DE MATRICES
1ª Conmutativa: A + B = B + A
2ª Asociativa: ( A + B ) + C = A + ( B + C )
3ª Elemento neutro: 0 ( matriz cero o matriz nula ).
0 + A = A + 0 = 0
4ª Elemento simétrico: - A ( matriz opuesta de A ).
A + ( -A ) = ( -A ) + A = 0
La opuesta de la matriz A se obtiene cambiando de signo todos los elementos de la matriz A: - (aij) = (-aij).
| |
4.2.4 Matriz inversa.
Cálculo de la matriz inversa usando determinantes
Dada una matriz cuadrada A, se llama matriz adjunta de A, y se representa por Adj(A), a la matriz de los adjuntos, Adj(A) = (Aij).

Si tenemos una matriz tal que de (A) ¹ 0, se verifica:
Esto es fácil probarlo puesto que sabemos que la suma de los productos de los elementos de una fila por sus adjuntos es el valor del determinante, y que la suma de los productos de los elementos de una fila por los adjuntos de otra fila diferente es 0 (esto sería el desarrollo de un determinante que tiene dos filas iguales por los adjuntos de una de ellas).

Método de Gauss-Jordan para el cálculo de la matriz inversa
El método de Gauss - Jordan para calcular la matriz inversa de una dada se basa en una triangularización superior y luego otra inferior de la matriz a la cual se le quiere calcular la inversa.

Para aplicar el método se necesita una matriz cuadrada de rango máximo. Sabemos que no siempre una matriz tiene inversa, por lo cual comprobaremos que la matriz tenga rango máximo al aplicar el método de Gauss para realizar la triangularización superior. Si al aplicar el método de Gauss (triangularización inferior) se obtiene una línea de ceros, la matriz no tiene inversa.

4.3 Determinantes
4.3.1 Definición de un determinante
El determinante es una herramienta matemática, se puede encontrar o extraer un determinante únicamente de las matrices que son cuadradas (tienen igual número de filas y columnas), y es un numero real (en caso de que la matriz sea real) consistente en la suma de los productos elementales de la matriz.
El orden de un determinante viene dado por el número de filas y columnas que tenga. Existen diferentes métodos para resolverlos, que veremos a continuación.

Nota: Es necesario indicar que usaremos los símbolos Det(A) o │A│ para referirnos al determinante de A.
El determinante de una matriz puede ser positivo, negativo o cero.
Leer más: http://www.monografias.com/trabajos101/determinates-algebra-lineal/determinates-algebra-lineal.shtml#ixzz3sFEh1nDU
4.3.2 Expansión por cofactores.
4.3.3 Propiedades de los determinantes.
Propiedades
- El determinante de una matriz es un invariante algebraico, lo cual implica que dada una aplicación lineal todas las matrices que la represente tendrán el mismo determinante. Eso permite definir el valor del determinante no sólo para matrices sino también para aplicaciones lineales.
- El determinante de una matriz y el de su traspuesta coinciden:

- Una aplicación lineal entre espacios vectoriales es invertible si y sólo si su determinante no es nulo. Por lo tanto, una matriz con coeficientes en un cuerpo es invertible si y sólo si su determinante es no nulo.
Determinante del producto
- Una propiedad fundamental del determinante es su comportamiento multiplicativo frente al producto de matrices:
Esta propiedad es más trascendente de lo que parece y es muy útil en el cálculo de determinantes. En efecto, supongamos que queremos calcular el determinante de la matriz  y que
y que 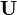 es cualquier matriz con determinarte uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con determinarte uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
 y que
y que 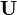 es cualquier matriz con determinarte uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con determinarte uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
Una aplicación lineal entre dos espacios vectoriales de dimensión finita se puede representar mediante una matriz. La matriz asociada a la composición de aplicaciones lineales entre espacios de dimensión finita se puede calcular mediante el producto de matrices. Dadas dos aplicaciones lineales 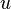 y
y  , se cumple lo siguiente:
, se cumple lo siguiente:
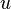 y
y  , se cumple lo siguiente:
, se cumple lo siguiente:Matrices en bloques
Sean  matrices
matrices  respectivamente. Entonces
respectivamente. Entonces
 matrices
matrices  respectivamente. Entonces
respectivamente. Entonces Esto se puede ver de la fórmula de . Empleando la siguiente identidad
Esto se puede ver de la fórmula de . Empleando la siguiente identidad
vemos que para una matriz general, A y D deben ser cuadradas y A regular.
Análogamente, se puede obtener una identidad similar con  factorizado.8
factorizado.8
 factorizado.8
factorizado.8
Si 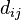 son matrices diagonales,
son matrices diagonales,
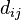 son matrices diagonales,
son matrices diagonales,Derivada de la función determinante
La función determinante puede definirse sobre el espacio vectorial formado por matrices cuadradas de orden n. Dicho espacio vectorial puede convertirse fácilmente en un espacio vectorial normado mediante la norma matricial, gracias a lo cual dicho espacio se convierte en un espacio métrico y topo-lógico, donde se pueden definir límites e incluso derivadas. El determinante puede definirse como un morfinismo del álgebra de las matrices al conjunto de los elementos del cuerpo sobre el que se definen las matrices:
El diferencial de la función derivada viene en términos de la matriz de adjuntos:
Donde:
 es la matriz de adjuntos.
es la matriz de adjuntos.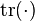 , es la traza de la matriz.
, es la traza de la matriz.
4.3.4 Regla de Cramer
Un sistema de ecuaciones lineales recibe el nombre de sistema de Cramer cuando se cumplen las dos condiciones siguientes:
- El número de ecuaciones es igual al número de incógnitas.
- El determinante de la matriz de los coeficientes (matriz del sistema) es distinto de cero ( det ( A ) # 0 )
Un sistema de Cramer es, por definición, compatible determinado, puesto que se cumple que rango (A) = rango (A*) = n (nº de incógnitas).
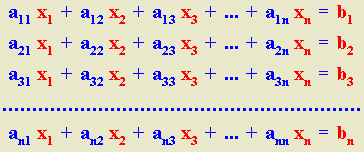
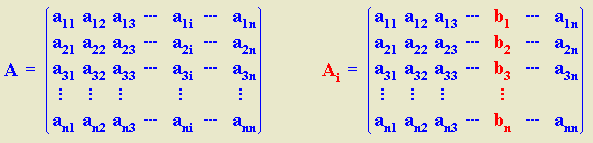
Consideremos un sistema de Cramer, es decir, un sistema de n ecuaciones lineales con n incógnitas, cuya expresión general es la siguiente:

Sean A la matriz del sistema (matriz de los coeficientes), entonces det (A) # 0. Llamaremos matriz asociada a la incógnita xi y la designaremos por Ai a la matriz que se obtiene al sustituir en la matriz del sistema la columna i por la matriz columna de los términos independientes. Es decir:

Todos los sistemas de Cramer son compatibles determinados. El valor de cada incógnita se obtiene dividiendo el determinante de la matriz asociada a dicha incógnita por la matriz del sistema (matriz de los coeficientes de las incógnitas).
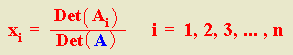

CONCLUSIÓN:
En este último modulo vimos cómo hacer los sistemas de ecuaciones y sus diferentes formas de resolverlo como por el meto de suma y resta, método de igualación, por sustitución, determinante.
Y en cada de uno de estos se tenían que realizar operaciones diferentes y que a fin de cuentas en todas tiene que darte el mismo resultado.
El álgebra matricial, vimos cómo hacer sumas, restas, multiplicaciones, y cuáles eran las condiciones para resolverlas y los diferentes pasos para cada operación; cuando comenzamos a entender más esto empezamos a realizar ejercicios en los cuales te decía la información que tenías que utilizar para resolverlo en forma de matriz.
Por ultimo vimos la inversa de una matriz que es muy distinto a la matriz original, la regla de Cramer la adjunta de una matriz, donde en todas seguían siendo matrices solo lo que cambiaba el método para resolverlo.
DERECHOS DE AUTOR:
Sistema de ecuaciones lineales. (2015, 9 de noviembre). Wikipedia, La enciclopedia libre. Fecha de consulta: 16:25, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Sistema_de_ecuaciones_lineales&oldid=86669241
DERECHOS DE AUTOR:
Jorge Cogollo. (13-dic-2013). ECUACIONES LINEALES - Ejercicios resueltos. 22-nov-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=LDJCl59hX7c
DERECHOS DE AUTOR:
Joanemarie28. (03 de septiembre de 2011). Sistemas de ecuaciones lineales. 22/11/2015, de SLIDESHARE Sitio web: http://es.slideshare.net/Joanemarie28/sistemas-de-ecuaciones-lineales-9123694.
DERECHOS DE AUTOR:
Ignacio Rosales Ortiz, Profesor en Universidad de los Ángeles. (23 de mayo de 2009). MÉTODOS DE SOLUCIÓN PARA UN SISTEMA DE ECUACIONES DE 2X2. 22/nov/2015, de Slideshare Sitio web: http://es.slideshare.net/Igneigna/mtodos-de-solucin-para-un-sistema-de-ecuaciones-de-2x2.
DERECHOS DE AUTOR:
Alfredo Pena Iglesias. (2006). SISTEMAS DE ECUACIONES LINEALES: CRITERIOS DE EQUIVALENCIA. 22-NOV-2015, de Descartes 3D Sitio web: http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_de_ecuaciones_lineales_2bcnt/equivalencia_de_sistemas_de_ecuaciones_lineales.htm.
DERECHOS DE AUTOR:
Eliminación de Gauss-Jordan. (2015, 20 de noviembre). Wikipedia, La enciclopedia libre. Fecha de consulta: 17:02, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Eliminaci%C3%B3n_de_Gauss-Jordan&oldid=87059222.
DERECHOS DE AUTOR:
Tareasplus. (28-NOV-2012). Sistemas de ecuaciones homogéneos. Parte 1. 22-NOV-2015, de www.youtube.com Sitio web: https://www.youtube.com/watch?v=NMg4ArT2C5E
DERECHOS DE AUTOR:
Sistema de ecuaciones lineales. (2015, 9 de noviembre). Wikipedia, La enciclopedia libre. Fecha de consulta: 16:25, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Sistema_de_ecuaciones_lineales&oldid=86669241
DERECHOS DE AUTOR:
Jorge Cogollo. (13-dic-2013). ECUACIONES LINEALES - Ejercicios resueltos. 22-nov-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=LDJCl59hX7c
DERECHOS DE AUTOR:
Joanemarie28. (03 de septiembre de 2011). Sistemas de ecuaciones lineales. 22/11/2015, de SLIDESHARE Sitio web: http://es.slideshare.net/Joanemarie28/sistemas-de-ecuaciones-lineales-9123694.
DERECHOS DE AUTOR:
Ignacio Rosales Ortiz, Profesor en Universidad de los Ángeles. (23 de mayo de 2009). MÉTODOS DE SOLUCIÓN PARA UN SISTEMA DE ECUACIONES DE 2X2. 22/nov/2015, de Slideshare Sitio web: http://es.slideshare.net/Igneigna/mtodos-de-solucin-para-un-sistema-de-ecuaciones-de-2x2.
DERECHOS DE AUTOR:
Alfredo Pena Iglesias. (2006). SISTEMAS DE ECUACIONES LINEALES: CRITERIOS DE EQUIVALENCIA. 22-NOV-2015, de Descartes 3D Sitio web: http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_de_ecuaciones_lineales_2bcnt/equivalencia_de_sistemas_de_ecuaciones_lineales.htm.
DERECHOS DE AUTOR:
Eliminación de Gauss-Jordan. (2015, 20 de noviembre). Wikipedia, La enciclopedia libre. Fecha de consulta: 17:02, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Eliminaci%C3%B3n_de_Gauss-Jordan&oldid=87059222.
DERECHOS DE AUTOR:
Tareasplus. (28-NOV-2012). Sistemas de ecuaciones homogéneos. Parte 1. 22-NOV-2015, de www.youtube.com Sitio web: https://www.youtube.com/watch?v=NMg4ArT2C5E
DERECHOS DE AUTOR:
Matriz (matemáticas). (2015, 20 de noviembre). Wikipedia, La enciclopedia libre. Fecha de consulta: 17:26, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Matriz_(matem%C3%A1ticas)&oldid=87066618.
DERECHOS DE AUTOR:
Matemáticas/Matrices/Tipos de matrices. (2015, noviembre 12). Wikilibros, . Consultado el 17:34, noviembre 22, 2015 en https://es.wikibooks.org/w/index.php?title=Matem%C3%A1ticas/Matrices/Tipos_de_matrices&oldid=292832.
DERECHOS DE AUTOR:
8CIFRAS. (26-ENERO-2014). Definición de matriz y tipos de matrices.. 22-NOV-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=AIoa_aTOrh8
DERECHOS DE AUTOR:
Harold Alvarez. (24-MARZO-2014). Operaciones con Matrices - Suma, Resta, Escalar por matriz. 22-NOV-2015, de WWW.YOUTUBE.COM Sitio web: https://www.youtube.com/watch?v=T8Upjb6Ep2Q
DERECHOS DE AUTOR:
José Ríos Saldaña. (1998). Cálculo de la matriz inversa. 22-nov-2015, de Rincon del vago Sitio web: http://html.rincondelvago.com/calculo-de-la-matriz-inversa.html
DERECHOS DE AUTOR:
Mateo Caldas Calle. (2001-2004). Determinantes Álgebra Lineal. 22-NOV-2015, de MONOGRAFIAS.COM Sitio web: http://www.monografias.com/trabajos101/determinates-algebra-lineal/determinates-algebra-lineal.shtml#bibliograa
DERECHOS DE AUTOR:
Determinante (matemática). (2015, 15 de octubre). Wikipedia, La enciclopedia libre. Fecha de consulta: 18:24, noviembre 22, 2015 desde https://es.wikipedia.org/w/index.php?title=Determinante_(matem%C3%A1tica)&oldid=85844619
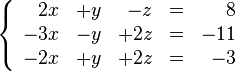


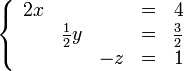

![\left [
\begin{array}{rrrr}
2 & 1 & -1 & 8 \\
-3 & -1 & 2 & -11 \\
-2 & 1 & 2 & -3
\end{array}
\right ]](https://upload.wikimedia.org/math/b/7/5/b75b0e02a527cf69e6f42dbd2fe2960f.png)
![\left [
\begin{array}{rrrr}
2 & 0 & 0 & 4 \\
0 & 1/2 & 0 & 3/2 \\
0 & 0 & -1 & 1
\end{array}
\right ]](https://upload.wikimedia.org/math/e/b/f/ebf74f6593b310153d2a6700d2f37b43.png)
![\left [
\begin{array}{rrrr}
1 & 0 & 0 & 2 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & -1
\end{array}
\right ]](https://upload.wikimedia.org/math/d/4/0/d40cfce339ef9bb6dde8739c55d238d3.png)
![\left [ \begin{array}{cccc}
0 & 0 & 0 & a \\
\end{array} \right ]](https://upload.wikimedia.org/math/4/e/a/4ea82b742b346fc121881fd94c0d3d0c.png)
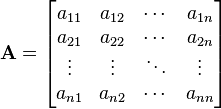
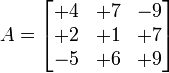


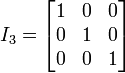
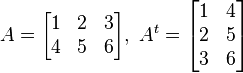

 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21
 =
=




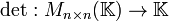

Tu blog me parece de mucha importancia, ademas de que en el pusiste información muy buena, la combinación de imágenes y colores de letra llaman la atención.
ResponderEliminarMuy buen blog, la información es clara y ayuda más a la comprensión
ResponderEliminarMuy buen blog ademas de que esta muy bien explicado la información es muy clara y los vídeos también están muy explicados.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarMuy buen blog, me gusto mucho, tienes buena información en cada tema en especifico y los videos que hay en tu blog son muy entendibles, excelente trabajo.
ResponderEliminarMuy buen blog, me gusta la combinación de información y videos en algunos temas ya que ayuda a que sea más entendible y dinámico, tiene buen orden y en cuestión de información está muy completo.
ResponderEliminarExcelente trabajo, el orden, los colores, las letras, tu informacion muy detallado todo gaby.
ResponderEliminarMe pareció totalmente perfecto. muy buen trabajo, cada tema me ayuda en la comprensión de cada duda que tenia, y además con los hipervínculos aclare mejor mis dudas.
ResponderEliminarMuy buen blog, se comprende muy bien el tema y los videos muy claros se nota la dedicacion y el desempeño que expresastes en el.
ResponderEliminarmuy buen blog la información esta muy bien explicada, ademas de que consideraste muy buenos videos para entender los temas de esta unidad
ResponderEliminarme gusto muxo tu blog, ya que tiene excelente informacion al igual que los videos son muy entendibles y todo muy bn ordenado.
ResponderEliminarGaby, muy bien blog, toda la información ordenada de la mejor manera, cada tema explicado a su totalidad, y los videos ayudan mucho para entender y aprender de otra manera más dinámica y simple los diferentes tipos de matrices y explicas muy bien cada tipo de matrices que vimos durante el curso.
ResponderEliminarExcelente trabajo Gaby.
Felicidades.
Gabrieelaaaaa, estoy sorprendido! hasta ahora es uno de los mejores blogs que he visto del curso (es el primero que veo jejejejeje, ntc xD )
ResponderEliminarDe verdad se nota con solo verlo que se le invirtió mucho trabajo y tiempo a este blog, la información más que completa, todo muy bien ordenado y muchos detalles extra como algunas imágenes que llaman la atención. Los resúmenes muy bien expresados por cierto... Felicidades administradora!
Buen blog, la información es muy precisa y los videos te ayudan a tener una mejor comprensión y así realizar de manera correcta los ejercicios
ResponderEliminarFelicidades.! Sorprendida con tu trabajo, asi de super waoo
ResponderEliminarMe encantaron tus imagenes en 3D, tu informacion y tus videos explicados en su totalidad, para entender y aprender de una manera dinámica(:
valla me quede impactada, esta padrísimo tu blog me encanto, la información es muy comprensible y junto con los videos se fortalece aun mas. FELICIDADES
ResponderEliminarExcelente blog
Gaby!! No cabe duda de la excelente alumna que eres es uno de los mejores trabajos que e visto me encanto la informacion que pusiste me parecio bastante interesante la del modulo 4 supiste desarrollar completamente los temas te felicito porque los videos son perfectos para el entendimiento de verdad que buen trabajo gaby me encanto !!
ResponderEliminarMuchas felicidades por tu blog GABY.
ResponderEliminarLo eh encontrado muy interesante y me ha aportado bastante ayuda para aclarar procedimientos y temas que creí serían más complicados. Muy buenas imágenes e hipervínculos.
gaby muy buen blog felicidades muy clara y confiable tu informacion me gusto como desenglosaste cada tema muchas felicidades buen trabajo
ResponderEliminarMuy convincente tu información, muy buen blog
ResponderEliminarexcelente blog gaby
ResponderEliminartoda tu informacion esta muy completa a los temas que vimos. Felicidades
Y el 4.4 😖
ResponderEliminar